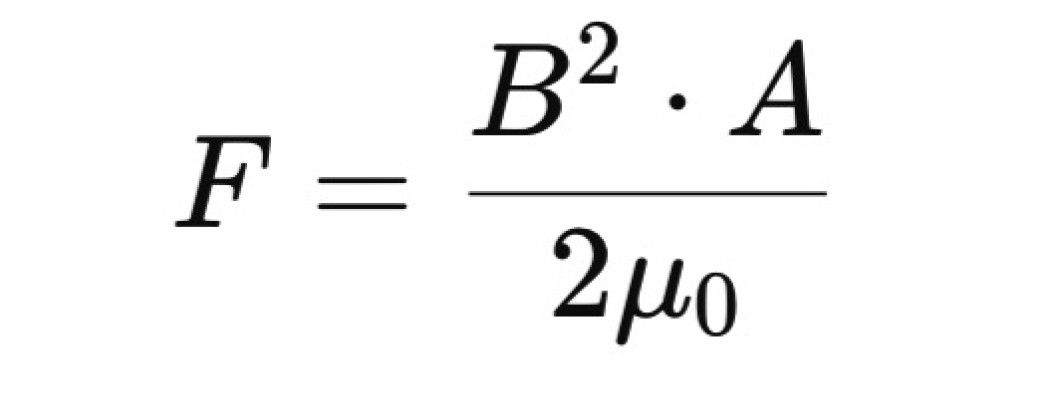
Permanens mágnes - számítások

Permanens mágnesek esetében több fontos fizikai jellemzőt is számolhatunk, amelyek segítenek megérteni és optimalizálni azok alkalmazását különféle területeken. Itt van néhány alapvető képlet, amelyek a leggyakrabban használt mágneses értékek kiszámítására szolgálnak:

1. Mágneses Fluxussűrűség (B)

Ahogy korábban említettem, a mágneses fluxussűrűség egy permanens mágnesnél a mágnesítettség és a vákuum permeabilitásának függvénye. A következő egyenlet használható:

$B={\mu }_0\cdot H$

ahol:

• ${\mu }_0$ a vákuum permeabilitása,
• $H$ a mágneses térerősség, amely arányos a mágnes anyagának mágneses polarizációjával $M$ (a mágnes saját mágneses mezője).

2. Mágneses Térerősség (H)

A mágneses térerősség a következőképpen számolható:

$H=\frac{B}{{\mu }_0}-M$

Ez azt mutatja, hogy mekkora a mágneses mező erőssége, amit a mágnes bocsát ki.

3. Mágneses Polarizáció (J)

A mágneses polarizáció, ami a mágnes mágneses momentumának sűrűsége:

$J=M\cdot {\mu }_0$

ahol $M$ a mágnes mágnesítettsége.

4. Mágneses Energiasűrűség (U)

A mágneses energiasűrűség, amely meghatározza, hogy mennyi energiát képes tárolni a mágnes térfogategységére vonatkoztatva:

$U=\frac{1}{2}B\cdot H$

Ez a képlet segít megérteni, milyen hatékonyan tárol a mágnes energia formájában mágneses teret.

5. Koercivitási Erő (H_c)

A koercivitási erő a mágneses mező erősségét jelzi, amely szükséges a mágnes teljes demagnetizálásához:

$H_c$ (megadott érték a mágnes adatai között)

Ez alapvetően az a mezőerősség, amelyet a mágnes ellenáll, mielőtt teljesen demagnetizálódna.

Példák

Ezeket az egyenleteket különféle helyzetekben lehet alkalmazni, mint például a mágneses mezők tervezése vagy mágneses eszközök optimalizálása. A képletek segíthetnek a mágnesek választásában és a műszaki specifikációk megértésében is.